Simplex category
In mathematics, the simplex category (or simplicial category or ordinal category) is the category of finite ordinals and order preserving maps. It is used to define simplicial and cosimplicial objects.
Formal definition
The simplex category is usually denoted by  and is sometimes denoted by Ord. There are several equivalent descriptions of this category.
and is sometimes denoted by Ord. There are several equivalent descriptions of this category.  can be described as the category of finite ordinals as objects, thought of as totally ordered sets, and order preserving functions as morphisms. The category is generated by coface and codegeneracy maps, which amount to inserting or deleting elements of the orderings. (See simplicial set for relations of these maps.)
can be described as the category of finite ordinals as objects, thought of as totally ordered sets, and order preserving functions as morphisms. The category is generated by coface and codegeneracy maps, which amount to inserting or deleting elements of the orderings. (See simplicial set for relations of these maps.)
A simplicial object is a presheaf on  , that is a contravariant functor from
, that is a contravariant functor from  to another category. For instance, simplicial sets are contravariant with codomain category the category of sets. A cosimplicial object is defined similarly as a covariant functor originating from
to another category. For instance, simplicial sets are contravariant with codomain category the category of sets. A cosimplicial object is defined similarly as a covariant functor originating from  . Note that in topology a simplicial object defined in this way would be called an augmented simplicial object because of the presence of an augmentation map. This map can be dropped to yield a traditionally defined simplicial object.
. Note that in topology a simplicial object defined in this way would be called an augmented simplicial object because of the presence of an augmentation map. This map can be dropped to yield a traditionally defined simplicial object.
An algebraic definition identifies  as the freely generated monoidal category on a single monoidal generator. This description is useful for understanding how any comonoid object in a monoidal category gives rise to a simplicial object since it can then be viewed as the image of a functor from
as the freely generated monoidal category on a single monoidal generator. This description is useful for understanding how any comonoid object in a monoidal category gives rise to a simplicial object since it can then be viewed as the image of a functor from 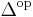 to the monoidal category containing the comonoid. Similarly, this also illuminates the construction of simplicial sets from monads (and hence adjoint functors) since monads can be viewed as monoid objects in endofunctors categories.
to the monoidal category containing the comonoid. Similarly, this also illuminates the construction of simplicial sets from monads (and hence adjoint functors) since monads can be viewed as monoid objects in endofunctors categories.
References
- P. G. Goerss and J. F. Jardine, Simplicial Homotopy Theory, Progress in Mathematics Vol. 174, Birkhäuser Basel-Boston-Berlin (1999) ISBN 3-7643-6064-X